
Understanding Square Roots and their Connection to √5
Have you ever wondered what a square root is and how it relates to the number √5? In this article, we will dive deep into the concept of square roots and explore their connection to the square root of 5, √5.
What is a Square Root?
A square root is a mathematical operation that determines the value that, when multiplied by itself, gives a certain number. For example, the square root of 25 is 5 because 5 multiplied by itself equals 25. The symbol used to denote a square root is √.
Exploring the Square Root of 5, √5
The square root of 5, denoted as √5, is an irrational number, meaning it cannot be expressed as a simple fraction or a finite decimal. It is approximately equal to 2.23607.
Properties of √5
- √5 is an irrational number, which means its decimal representation goes on infinitely without repeating.
- √5 is a non-terminating, non-repeating decimal.
- √5 is greater than 2 but less than 3.
- When √5 is squared, it results in the number 5.
Application of √5
The square root of 5, √5, finds its applications in various fields, such as geometry, engineering, and finance.
In geometry, the square root of 5 plays a significant role in calculating the diagonal of a square with sides measuring 1 unit. The diagonal can be calculated using the formula D = a√5, where D represents the diagonal length and a represents the side length of the square.
In the field of finance, the square root of 5 is employed in the calculation of financial ratios and portfolio risk management models. Its inclusion in these calculations helps to determine asset volatility and potential investment returns.
Conclusion
Square roots are essential mathematical operations that allow us to find numbers that, when multiplied by themselves, yield a given value. The square root of 5, √5, is an irrational number that holds significant value in various disciplines, including geometry and finance. Although it cannot be expressed as a simple fraction or finite decimal, it is a crucial component in numerous calculations.
By understanding the concept of square roots and their relation to √5, we can unlock new insights and applications in the world of mathematics and beyond.
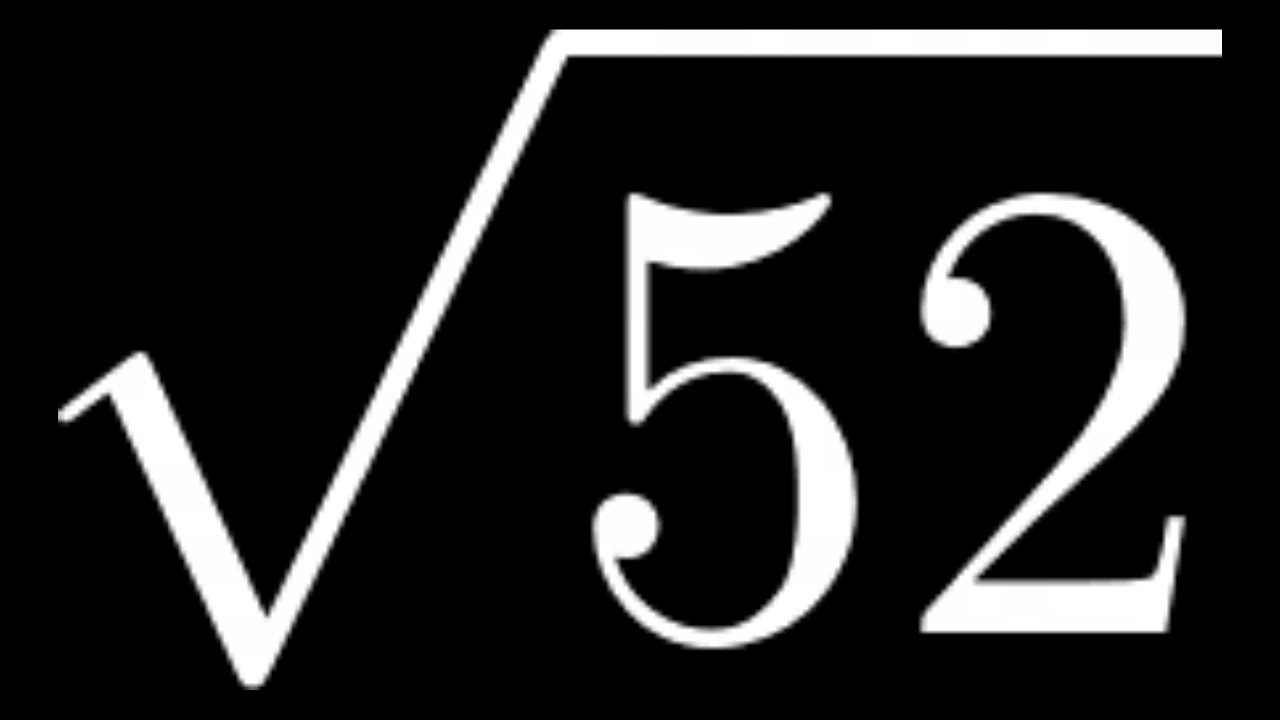
Calculating the Square Root of 52: Strategies and Methods
Introduction
Are you looking to calculate the square root of 52? Look no further! In this article, we will explore various strategies and methods to help you effortlessly determine the square root of this number. Whether you’re a math enthusiast or just someone in need of this specific calculation, we’ve got you covered.
1. Method 1: Traditional Calculation
If you prefer a traditional approach to finding square roots, then this method is for you. Begin by estimating the closest perfect square value near 52, which is 49. Now, divide 52 by 49 to get a rough approximation of the square root. In this case, the result is approximately 1.06.
2. Method 2: Using Scientific Calculators
If you want a more accurate calculation, a scientific calculator can be your best friend. Most standard calculators have a square root function. Simply input the number 52 and press the square root button, and voila! The calculator will give you the precise square root value, which is approximately 7.211.
3. Method 3: Online Square Root Calculators
In the era of technology, online calculators are just a click away. Numerous websites offer free square root calculators that provide quick and accurate results. Simply search for square root of 52 calculator on your preferred search engine, and choose a reliable website to perform the calculation. With this digital tool, you’ll get the square root value faster than you can say mathematics.
4. Method 4: Approximation Techniques
If a precise value is not your priority, approximation techniques can be your go-to strategy. One such technique is the Newton-Raphson method, which includes multiple iterations to refine an initial guess. Although it requires more mathematical knowledge, it can provide a close approximation of the square root value.
Conclusion
Now that you are equipped with various strategies and methods for calculating the square root of 52, you can choose the approach that suits you best. Whether you prefer traditional calculations, scientific calculators, online tools, or approximation techniques, rest assured that finding the square root won’t be a hassle anymore. Happy calculation and enjoy exploring the fascinating realm of mathematics!
Note: Please keep in mind that accuracy may vary depending on the method used and the level of approximation. It’s always recommended to double-check your results and consult with a mathematical expert if required.
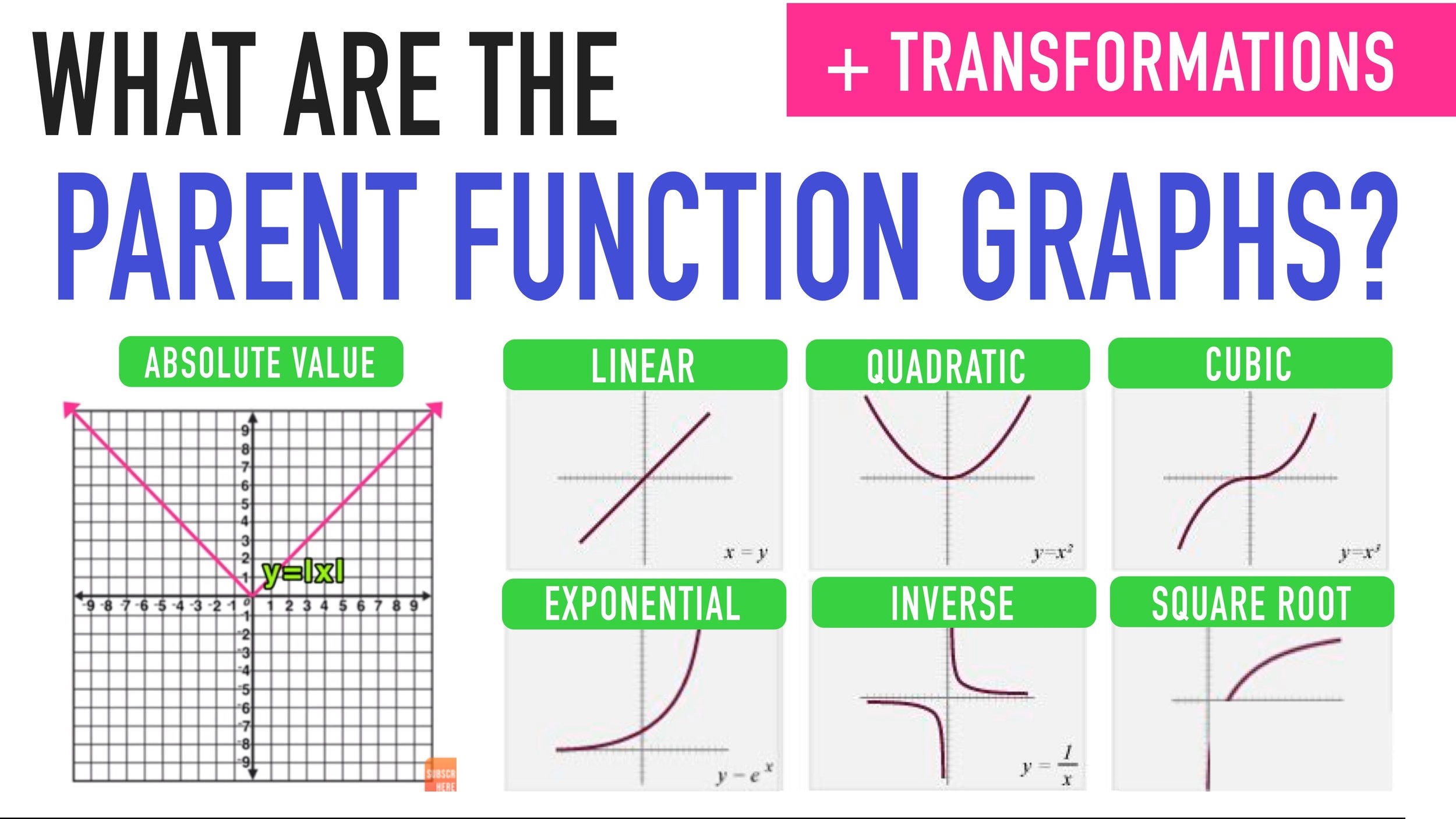
The Significance and Applications of Root 5 in Mathematics and Beyond
Introduction
Root 5 is a fundamental mathematical concept that holds significant implications not only within the realm of mathematics but also in various other fields. In this article, we will explore the significance and applications of root 5, shedding light on its role in mathematics and beyond.
Understanding Root 5
Root 5 is an irrational number that is denoted as √5 or 5^(1/2). As an irrational number, it cannot be expressed as a fraction or a decimal. Instead, it is an infinite non-repeating sequence of numbers, making it a mysterious and intriguing mathematical entity.
The Golden Ratio and Fibonacci Sequence
Root 5 is closely related to the famous Golden Ratio, often represented by the Greek letter Phi (Φ). The Golden Ratio is approximately equal to 1.618 and is obtained by dividing a line into two parts in such a way that the ratio of the whole line to the longer segment equals the ratio of the longer segment to the shorter segment.
Root 5 is also connected to the fascinating Fibonacci sequence, a series of numbers in which each number is the sum of the two preceding ones (e.g., 0, 1, 1, 2, 3, 5, 8, 13, 21, and so on). As the sequence progresses, dividing each number by its predecessor or successor gradually approximates the value of root 5, showcasing its prevalence in nature and aesthetics.
Applications in Mathematics
Root 5 finds various applications within the field of mathematics. It is often used in equations involving quadratic functions, geometry, and trigonometry. Understanding root 5 helps to solve complex mathematical problems and aids in the exploration of mathematical concepts.
Applications in Science and Nature
The significance of root 5 transcends beyond mathematics and manifests in various scientific disciplines. It appears in patterns prevalent in natural formations such as the arrangement of leaves on a stem, the branching of trees, and the spiral arrangement of seeds in the sunflower. This connection to the natural world deepens our understanding of the underlying mathematical principles governing our universe.
Applications in Art and Design
Root 5 is renowned for its aesthetic appeal, making it a key element in art, design, and architecture. Its presence can be observed in famous artworks, ancient architectural structures such as the Pyramids of Egypt, and modern designs. Incorporating root 5 into artistic creations and designs often results in visually pleasing and harmonious compositions.
Conclusion
Root 5 holds immense significance and applications in mathematics, as well as in science, nature, art, and design. Its connection to the Golden Ratio, Fibonacci sequence, and its prevalence in various natural and man-made formations make it a captivating and versatile mathematical concept. Understanding and harnessing the power of root 5 opens doors to new avenues of knowledge and creativity, enriching our understanding of the world around us.
- Root 5 is an irrational number with significant implications.
- Its connection to the Golden Ratio and Fibonacci sequence is noteworthy.
- Applications exist in mathematics, science, nature, art, and design.
- Understanding root 5 unlocks new avenues of knowledge and creativity.
